Negative Integer Data Representation – Part 2

In part 2 of representing negative integers in data, we ask the question: What if we could represent the actual negative values by mapping a set of the bit range? In this episode, you’ll walk through the process.

Your key takeaways are:

• Split the range of available binary bit patterns in half
• The lower half are for positive integers
• The upper half are for negative integers
• To compute the negative integers, you flip the positive binary pattern and then add one
• Overflow happens when numbers are outside of the range

Study Notes

Split the Range in Half

How could we “map” half of the binary range for negative numbers?  With this system we are not assigning a negative or positive sign, but rather dealing with the actual values.

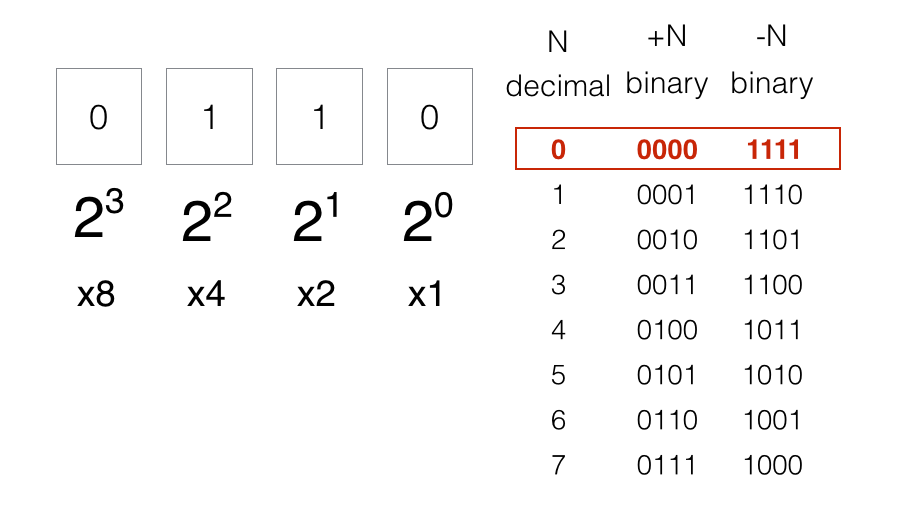In a 4-bit system, we have 4 bits which have positional values of 1 to 8.  This system gives us a number range from 0000 to 1111 or 0 to 16.  If we split this range in half, our numbers will be:

0000 to 0111, which we will assign to the positive numbers 0 to 7.

1000 to 1111 we will assign to the negative numbers -7 to 0.

Notice that the number ranges have a pattern: ordered by smallest to largest in the range.  In the positive numbers, zero is smaller than seven.  In the negative range, negative seven is smaller than zero.

Let’s lay this out into a table to view what we have.

The positive numbers are 0000 to 0111 and correspond respectively to the decimal numbers 0 to 7.  Next we lay in the negative numbers starting with the smallest number (-7) up to the largest (0).

What did you notice here?

1. The numbers start at zero go to seven and then go from -7 back up to zero.
2. Yes, we still have two zeros, but we will deal with this in the next iteration.
3. The negative binary are inverted versions of the positive bit patterns.

Case in point, look at decimal 2.  In positive binary, it is 0010.  In negative, flip the bits and you get 1101.

This is 1’s complement notation.

Rule in 1’s compliment: If there is a carry bit, then add it back into the pattern at the least significant bit.

How to deal with the negative and positive zeros?

What if we add a one to the negative binary pattern? Watch what happens here.

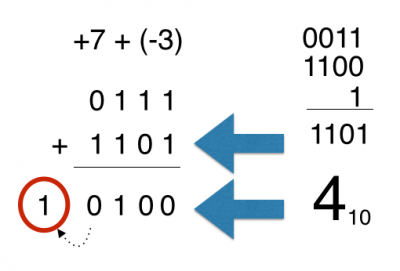Notice that we converted 1111 into 0000. Remapping our negative binary numbers, the double zero problem is gone.

We shifted our range of numbers by one. But now we only have 15 numbers. What do we do with 1000? It is -8. We increased our range then from -8 to 7.

Rule in 2’s compliment: Throw away the carry-over bit.

What about overflow?

What happens when adding two numbers together and the result is greater than the range of our number set?

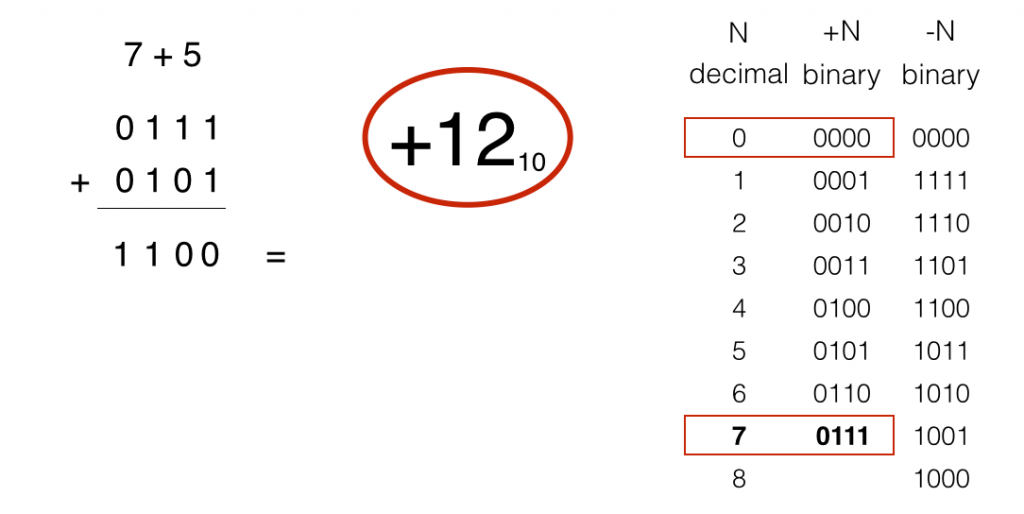
Let’s add 7 and 5 together.  The result is decimal 12.

But 12 is outside the range of the positive numbers.  The range goes from 0 to 7.

It’s a good indicator that something is wrong here, because we know a negative number’s pattern has a 1 in the most significant bit position.

When a number is outside of the range, it is called, “overflow.”

How is overflowed handled?  It causes an error.  This is exactly what we want to have happen because we want and expect accuracy.  If something goes wrong, then we need some sort of flag or indicator to alert us.

Why do we discuss “overflow”?

• The real world around us is infinite
• Data is continuously flowing
• Computers are finite
• We need a set of parameters to define expected behavior within a limited computer

Extra External References

• Binary: Plusses & Minuses