Number System for State

This episode continues our discussion on the Basics of Digitizing Data. Let’s talk about a numbering system that represents state, i.e. on or off and one or zero. It’s an introduction to binary.

Your key takeaways are:

• 0 and 1 are the simplest digits
• 1 represents a value, e.g. on, go, present, all clear, etc.
• 0 represents no value, e.g. off, stop, absence, not clear, etc.
• Digital signal is 0 or 1
• Combine 1s and 0s to represent counts (numbers)

Study Noties

What is the simplest way to communicate in a numbering system?

Think about this:  What are the simplest symbols, numbers, or digits?

How do we communicate state in our world?

To help us understand, let’s talk about how we communicate “state” in our world:

• ON or OFF
• Presence or Absence
• Go or No Go
• Clear or Not Clear

We use various language means to communicate a simplistic state.

How can we convert those visual representations for “state” into a numbering system?  What are the symbols we can use?

Think in digits

Using the same graphics as before, we’ll attach the proper digits to the “state.”

If a state is “off,” how can that be represented?  It has no value because it’s “off.”  Therefore, it is a 0 digit. Conversely, if the state is “on,” then it has value.  We can represent it as a 1 digit.

If something is present, it has value in contrast to not being present (or being absent.)   Therefore, we can say that presence is represented by a 1 digit and absence is represented by a 0 digit.

Sum it up

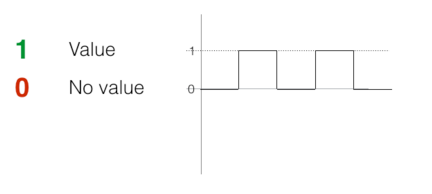Our symbol, which is a digit 1, means it has a “value.” It’s “on,” “present,” “go,” “all clear,” and any other state meaning “yes.”

Our symbol, which is a digit 0, means it does not have a “value.”  It’s “off,” “absence,” “stop,” or “not clear.”

Using our digital signal, we see that a 1 means the presence of electrical voltage—or power is flowing; whereas, a 0 means no power or electrical voltage is flowing.

Convert simple digits into a numbering system

In Decimal Number System

• 10 digits -> 0 to 9
• Base 10
• Collection of 10 items we can count

What do we know about our new numbering system?

• 2 digits -> 0 and 1
• Base ?
• Base 2
• Collection of 2 items we can count

In Decimal, we have 10 digits, or symbols.  And we said that was a base 10, or a collection of ten items that we counted.

Here we only have two digits. 0 and 1

What base do we call it?  If we called decimal base 10, what do we call this new numbering system? Base 2.

How many states can you represent with two digits?

Two

But we need more…

Pattern of 1s and 0s

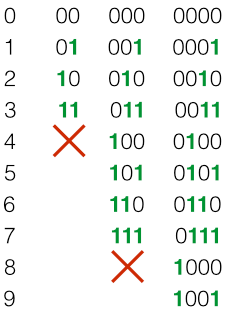
These are patterns using a combination of 1s and 0s. We are going to walk through the patterns of decimal to bit and binary conversion.  This is a preliminary to actually learning binary conversion.