Improving Binary Representation

In this episode, you are going to learn about how to improve the binary representation. Computer scientists and mathematicians found a way to look at the number pattern and intuitively read it to know what it represents.

The key takeaways from this episode are:

• Octal gives us a more efficient representation of 1s and 0s
• Base-8
• 8 digits 0-7
• Breaks binary into groups of three bits starting from LSB

Study Notes

Converting from binary to decimal?

There has to be an easier way.

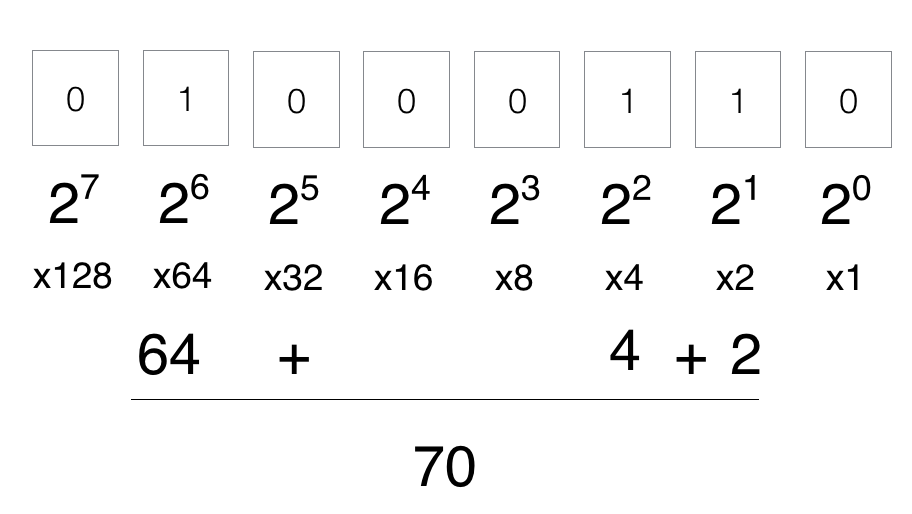
The process of converting binary to decimal takes a few steps.  It is more difficult to look at the pattern of 1s and 0s and pull out the exact decimal equivalent.

What if you could break down the patterns?

Base-8 or Octal

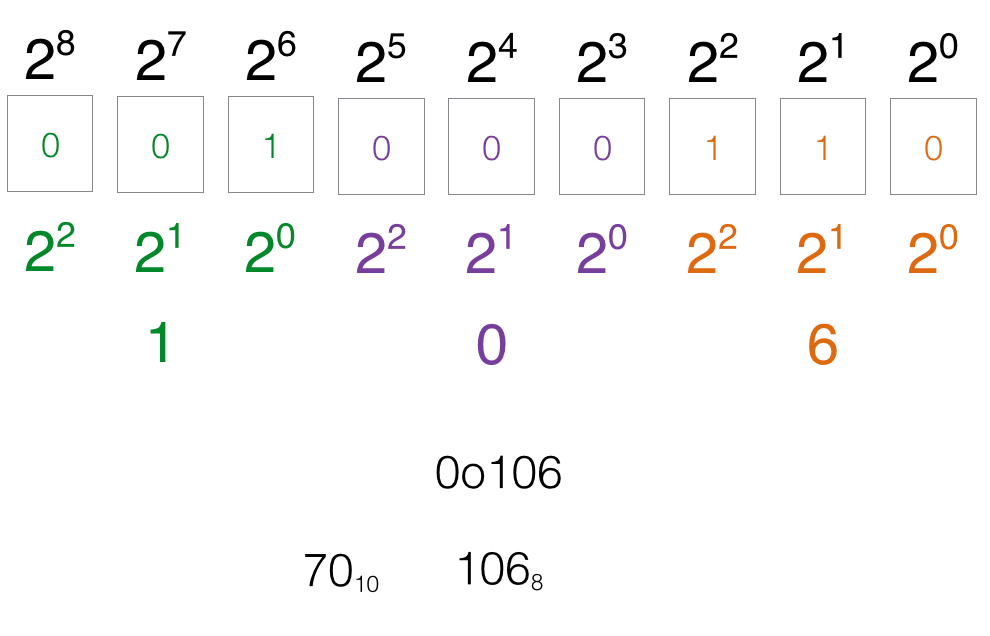
This is a base-8 number system, which is called octal.

We want to convert this binary pattern into octal.  How?

The first step is to divide up the binary into sets of three bits starting at the least significant bit (on the right).  If you end up with less than three on the left, then add zeros.

Octal represents just three bits that get combined together to form a new symbol.  You start at the least significant group of three bits and then convert that pattern into a digit.  Then repeat until you complete the entire binary number.

Notice that 106 looks just like the decimal 106.  However, you know that octal 106 is actually 70 in decimal (or base 10).  How do we differentiate the numbering systems?

Octal can be prefixed with a “0o” or suffixed with a “8”.  Both of these formats denote octal.

Why use Base-8 / Octal?

• Easier to visualize
• Easier to work with

Practical uses of Octal:

• File permissions under a Unix system are in Octal