The Age of 16 Bit and Hexadecimal

Let’s talk about the age of 16-bit and new numbering system. We need to compute larger numbers. Working in binary and octal is mind-numbing. Bam, welcome the hexadecimal (or hex) notation, which you use every day for CSS color codes.

Your key takeaways in this episode are:

• Hexadecimal (hex) more condensed notation
• Allows up 16 digits: 0-9 + A-F
• One hex notation is the same as 4-bit groupings in binary
• Useful for larger numbers
• Color codes use hex

Study Notes

Remember: Larger numbers = more power

The process of converting binary to decimal takes a few steps.  It is more difficult to look at the pattern of 1s and 0s and pull out the exact decimal equivalent.

Large Number Conversion

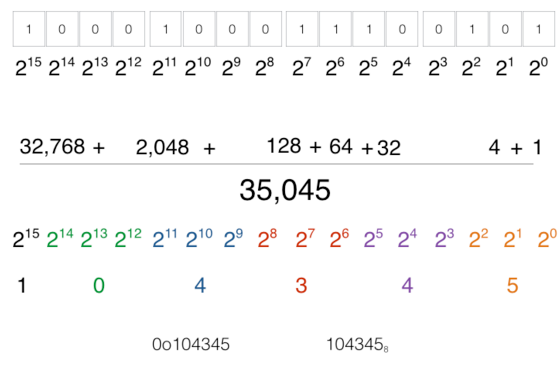
How can we simplify the representation?

New 16-bit Number System:

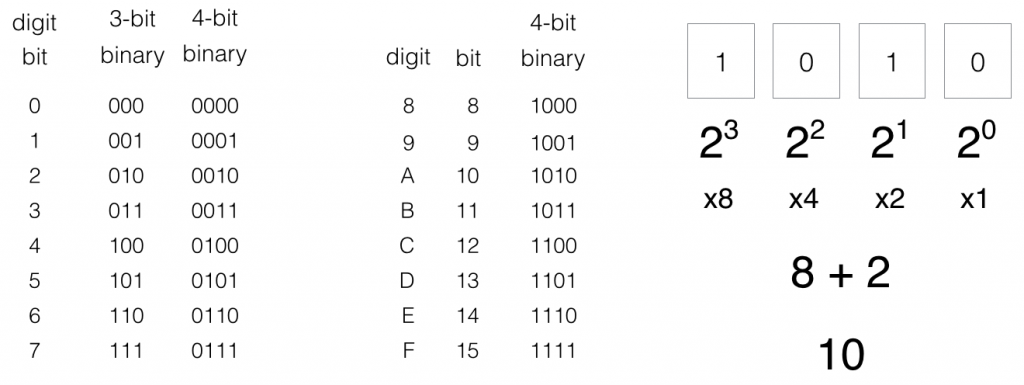
What are the building blocks of our new 16-bit number system?  Let’s start with octal.

In octal, we have seven bits which are also the digits 0-7.  It uses a grouping of 3-bit binary to represent the digits.

Notice that we’ve used all of the 1s and 0s patterns.

16-bit Conversion:

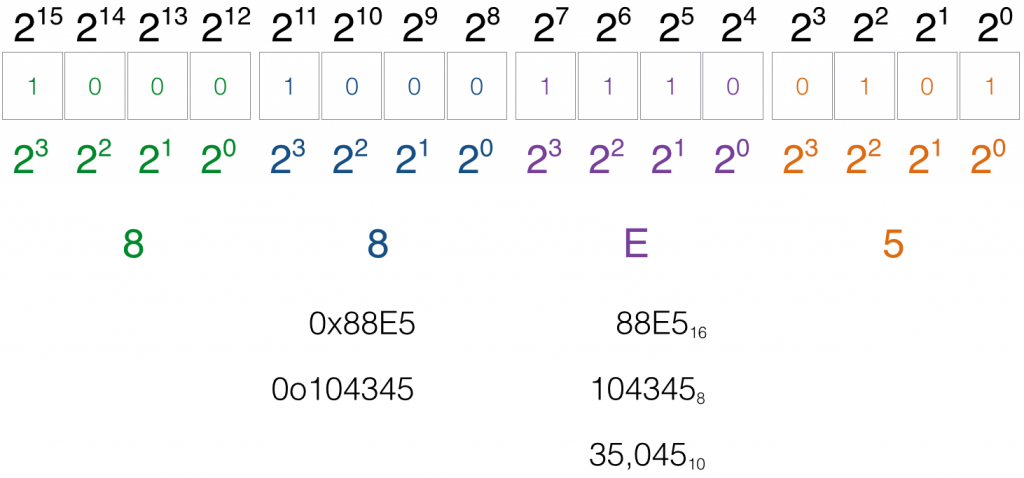
Let’s walk through converting this binary into our new 16-bit number system.  We group it by 4 bits, meaning there are 4 digits for a 2-byte binary pattern.  Always start at the least significant bit (to the far right.)

The notation of this new number is 0x1445, where the x denotes hex or hexadecimal.  The shorthand notation is 1455₁₆.

Now compare this new number notation with octal.  Do you see how using hex is a better form for larger numbers?

Wondering where you’ll ever use hex?

Color codes are done in hex.

Let’s convert the hex representation for the color “white” into binary, octal, and decimal formats.

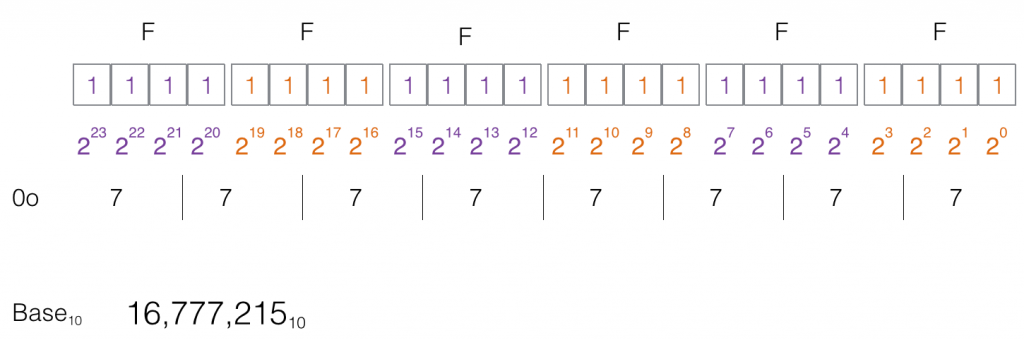
Practical uses of Hex

• Color codes
• Error messages
• Bar coding
• Communicating with APIs